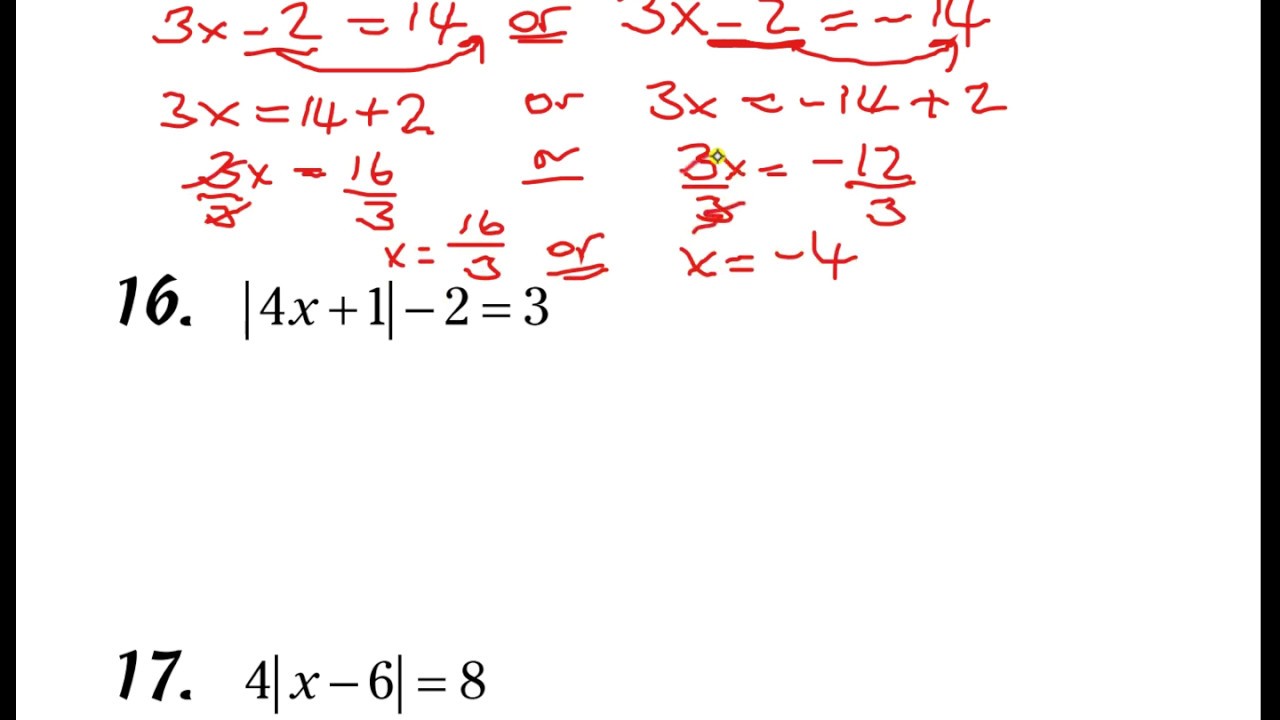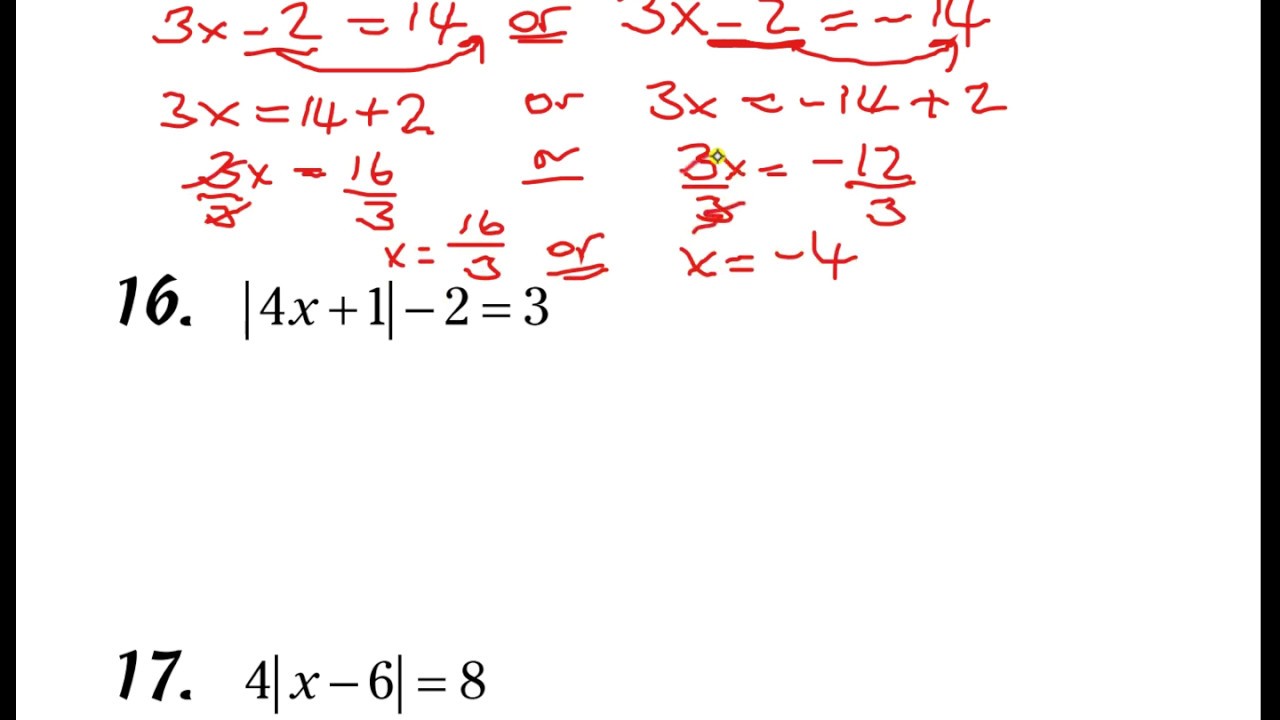Instruct that what is done on one side of the equation (= sign), must be done on the other side of the = sign. GOAL: to isolate the specified variable. Instruct that minus and negative are equivalent. Vocabulary: inverse operation, isolate, variable, constant, reciprocal, coefficient, absolute value bars, absolute value LESSON Do you treat absolute value equations any differently than regular equations? I can construct an argument to justify my solution processġ.What is the difference in solving a regular equation and an equation with variables on both sides?Ģ. I can apply order of operations and inverse operations to solve equations. Construct a viable argument to justify a solution method.Ī.REI.3: Solve linear equations and inequalities in one variable, including equations with coefficients represented by letters.ģ Construct viable arguments and critique the reasoning of others. Finally students will learn how to solve equations involving absolute value.Ī.REI.1: Explain each step in solving a simple equation as following from the equality of numbers asserted at the previous step, starting from the assumption that the original equation has a solution. Located at: License: Public Domain: No Known Copyright.Prior Knowledge: Students should have learned how to write equations, translate sentences into equations and equations into sentences, solve one-step equations using addition and subtraction, solve simple equations using multiplication or division, solve multi-step equations and solve equations with variables on both sides of the equation.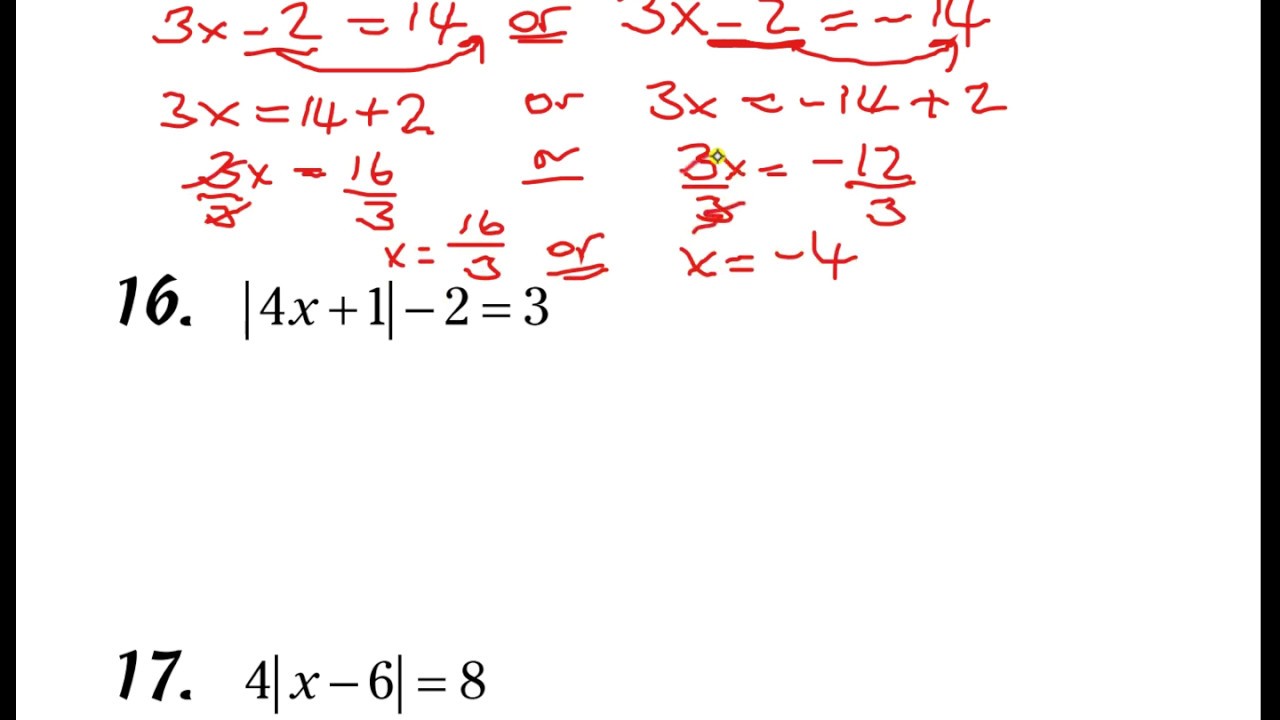 
License Terms: IMathAS Community License CC-BY + GPL Authored by: James Sousa () for Lumen Learning. License Terms: Download for free: Ex 4: Solving Absolute Value Equations (Requires Isolating Abs.
Ex 4: Solve and Graph Absolute Value inequalities (Requires Isolating Abs. Ex 2: Solve and Graph Absolute Value inequalities. 
Ex 1: Solve and Graph Basic Absolute Value inequalities. Notice absolute value is not alone, multiply both sides by the reciprocal of -\frac Answer
0 kommentar(er)
